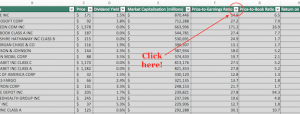
In the world of gambling and trading, Ed Thorpe is a legend. He is the man who essentially perfected card counting and managed to beat a roulette table with the help of the first handheld computer ever invented. Then he moved on to Wall Street starting one of the earliest quant funds in the business and pioneering fields like convertible arbitrage.
He wrote several books, including Beat the Dealer, all of which are worth reading for their entertainment value alone. But his greatest contribution to the world of trading is popularizing the Kelly Criterion which is essentially a formula for optimal bet size.
The mathematics for the Kelly Criterion along with a deep discussion of its various permutations can be found here. But if your eyes glaze over the moment you see a Greek letter, don’t worry, the key thing to take away from the Kelly Criterion principle is the idea of proportional betting.
The two cardinal sins of all traders are 1. Betting too large. 2. Increasing size when you have lost money. The Kelly Criterion deals with the first issue by calculating optimal opening size and deals with the second issue by betting only a fixed percentage of equity each time. This way when equity declines, the trader naturally trades smaller and when it rises the trader naturally increases size. This creates a disciplined structure to your trading without any conscious effort on your part.
But while the fundamental idea of proportional betting is truly one of the best practices in trading, the Kelly formula in its original form is full of problems. First of all, Kelly was designed for games with fixed outcomes and is, therefore, an imperfect fit for the open-ended world of trading where nothing is fixed and odds are perpetually shifting. People generally adjust for this reality by relying on the law of large numbers, but that idea assumes that you as a trader must survive ten’s of thousands of trades in order for the Kelly math to bear fruit. As Yogi Berra once said “In theory, there is no difference between practice and theory. In practice, there is.”