EC Time In The Market, Not Timing The Market? Catchy Phrase Ignores Key Evidence -

EC Time In The Market, Not Timing The Market? Catchy Phrase Ignores Key Evidence

Jul 19, 2017Jeremy ParkinsonFinance0

There is a reason why Warren Buffett regarded market-cap-to-GDP as “…the best single measure of where valuations stand at any given moment.” The reason? Its relationship with 10-year forward returns for stock prices. And right now, stock market capitalization as it relates to the U.S. economy is projecting negative returns for U.S. stock prices.

It is also true that Mr. Buffett has, in recent years, distanced himself from the valuation approach called the “Buffett Indicator.” Is it because he stopped believing that valuations matter? Probably not. In fact, the Oracle of Omaha is holding onto more cash than at any other quarter in the last decade.

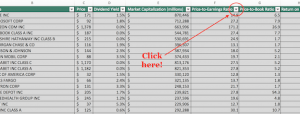
If market-cap-to-GDP is no longer in Warren Buffett’s good graces, do other valuation measures explain why he is holding onto record levels of cash in Berkshire Hathaway (BRK.B)? Hard to say. With the exception of tech bubble euphoria, U.S. stocks have never been more expensive on price-to-sales ratios (P/S), price-to-earnings ratios (P/E), dividend yield or Tobin’s Q.

Indeed, market-cap-to-GDP merely confirms what Mr. Buffett knows to be true. The higher the price one pays, the lower one’s return over time. Similarly, the lower the price one pays, the higher one’s return over time.

“But Gary,” you protest. “Nobody can time the market. Even Warren Buffett thinks people should buy-n-hold.”

In truth, Mr. Buffett is a market timer. He buys, sells, rebalances, increases his stakes, decreases his stakes and even completely divests from particular companies according to his discipline. He just does not think that others can time the market effectively.

Maybe he’s right. Maybe they can’t.

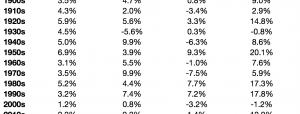
On the other hand, “market timing” with nothing more than a 10-month simple moving average and the 10-year Treasury has outperformed buy-n-hold with less risk.

This is worth repeating. Market timing with the 10-month simple moving average has outperformed buy-n-hold over the last 90 years. It has done so on a head-to-head basis. And more importantly for risk managers, it has done so on a risk-adjusted basis via standard deviation and the Sharpe ratio.