Investment sales firms like to point to multi-decade charts of smooth upward-sloping return lines as a way to forecast compound returns ad infinitum. Except, I don’t have a time horizon of infinity, and neither do you. In real life, credit driven contraction cycles and the math of loss are recurring snakes that define the return game for mortals. And since most people, acquire the bulk of their life savings late in their life, capital lost in down years, makes all the difference in the world–not only in terms of our mental health and financial stability–but also in terms of lasting net benefit for capital risk taken.
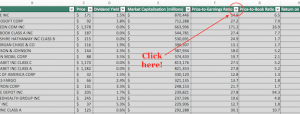
Let’s take this table of S&P annual total returns since 1987 courtesy of Ycharts.com.

Table source:
At a first glance, all seems very encouraging, with positive index returns in all but 5 of the last 29 years. Where do we sign, right? Stay tuned for some critical disclaimers.
First, total return numbers assume that every dividend received is reinvested quarterly without any fees being paid, withdrawals being made, or lump sums being added at any price peaks along the way. Why does this matter?Because without these fantastical assumptions, compound return numbers decline dramatically. But for the sake of argument, let’s work with these fantasy-best-possible-return assumptions for a moment.
Suppose for example, you were happily holding a chunk or your life savings in US stocks at their last secular valuation peak in December 1999, just in time for the mean reversion phase that saw prices decline over the next 3 years. Assuming you didn’t panic or need to sell and raise cash for any unforeseen reason, like say a job loss or business income decline, assuming you held on, prices began to recover in 2003, so no big deal right?
Well except, as shown above–if you were brave and held on, and didn’t pay any fees, or withdraw any cash or use any dividends to pay for anything at all–you still had to wait 7 years to December 2006 for your capital to grow back to where it started at December 1999. And that’s not all.