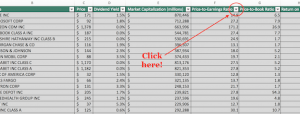
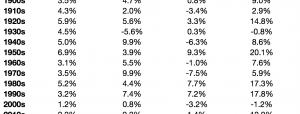
The superior performance of low-beta and low-volatility stocks was documented in the literature back in the 1970s — by Fischer Black (in 1972) among others — even before the size and value premiums were “discovered”. The low-beta/low-volatility anomaly has been demonstrated to exist in equity markets around the globe. I’ve already written about the low-volatility (i.e., low-risk or low-beta) anomaly before.
Idiosyncratic Volatility and the Beta Anomaly
Jianan Liu, Robert F. Stambaugh and Yu Yuan sought the answer to the puzzle that is the beta anomaly with their February 2017 paper, “Absolving Beta of Volatility’s Effects”. Because this paper builds on their 2015 paper, “Arbitrage Asymmetry and the Idiosyncratic Volatility Puzzle,” which appeared in the October 2015 issue of The Journal of Finance, I’ll first review the findings of that study, which addressed the anomaly that stocks with greater idiosyncratic volatility (IVOL) have produced lower returns. This is an anomaly because idiosyncratic volatility is viewed as a risk factor — greater volatility should be rewarded with higher, not lower, returns.
Liu, Stambaugh and Yuan begin with the hypothesis that IVOL represents risk that deters arbitrage and the resulting reduction of mispricings. They then combine this concept with what they term “arbitrage asymmetry” — the greater ability and/or willingness of investors to take a long position as opposed to a short position when they perceive mispricing in a security. This asymmetry occurs because there are greater risks and costs involved in shorting, including the potential for unlimited losses.
The figure below, which is from the paper, highlights the concept:

In addition to the greater risks and costs of shorting, for stocks with a low level of institutional ownership, there may not be sufficient shares available to borrow to sell short. Because institutions are the main lenders of securities, studies have found that when institutional ownership is low, the supply of stocks to loan tends to be sparse. Thus, short-selling tends to be more expensive. Furthermore, the charters of many institutions prevent, or severely limit, shorting. Finally, there is the risk that adverse moves can force capital-constrained investors to reduce their short positions before realizing profits that would ultimately result from corrections of mispricing. Importantly, when IVOL is higher, substantial adverse price moves are more likely. The authors write: “Combining the effects of arbitrage risk and arbitrage asymmetry implies the observed negative relation between IVOL and expected return”.
To see the effect of limits to arbitrage and arbitrage asymmetry, Stambaugh, Yu and Yuan note that stocks with greater IVOL, and thus greater arbitrage risk, should be more susceptible to mispricing that isn’t eliminated by arbitrageurs. Among overpriced stocks, the IVOL effect in expected return should therefore be negative. Stocks with the highest IVOL should be the most overpriced. However, with arbitrage asymmetry, the reverse isn’t true, as the greater willingness to buy (versus short) allows arbitrageurs to eliminate more underpricing than overpricing. The core results are highlighted in the following chart, again from the study, and show the hypothesized relationship between IVOL and mispricing.

The authors explain as follows:
As a result, the differences in the degree of underpricing associated with different levels of IVOL should be smaller than the IVOL-related differences in overpricing. That is, the negative IVOL effect among overpriced stocks should be stronger than a positive IVOL effect among underpriced stocks. When aggregating across all stocks, the negative IVOL effect should therefore dominate and create the observed IVOL puzzle.
Testing the Hypothesis
To test their hypothesis, Stambaugh, Yu and Yuan constructed a proxy for mispricing. Specifically, they established a composite measure averaging each stock’s rankings associated with 11 return anomalies that represent violations of the Fama-French three-factor (market beta, size and value) model: